Шиліна Математика

21 листопада 2024 року. Алгебра

Властивості степеня з натуральним показником.

Переглянь відео.

Виконай вправи:№335,338,341

22 листопада 2024 року. Геометрія. 

Властивості паралельних прямих.

При перетині двох паралельних прямих третьою січною:

 

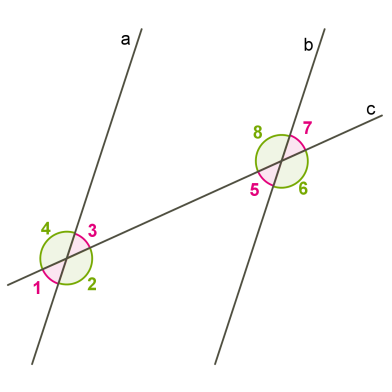
• внутрішні різносторонні кути рівні; 
   
• відповідні кути рівні;
   
• сума односторонніх кутів дорівнює 180°.

Виконай вправи №215,217

14 листопада2024 року. Алгебра

Степінь з натуральним показником.

Переглянь відео.

Виконай вправи: №300,302,305(1-3)

Геометрія.15 листопада 2024 року

Кути, утворені при перетині двох прямих січною

Переглянь відео.

Виконай вправи:№ 185,189

14.05.Координатна площина.

Французький філософ і математик Рене Декарт 

(1596−1650) у XVII ст. запропонував метод двох координат для знаходження точки на площині. Тому система координат названа його ім'ям.

Декартову систему координат утворюють:

 

1. Дві перпендикулярні прямі, на яких зазначено напрям зростання чисел. Горизонтальна пряма називається віссю Ox, або віссю абсцис. Вертикальна пряма називається віссю Oy, або віссю ординат.

  

2. Точка перетину прямих — початок координатної системи, яка часто позначається буквою O.

  

3. Відрізки на кожній осі завдовжки в одну одиницю вимірювання.

Для будь-якої точки знаходять дві координати x і y (абсциссу і ординату) й записують, як A(xA;yA).

№ 1563, 1565

09.05.Координатна площина.

№1547,1561

07.05.Перпендикулярні і паралельні прямі

Дві прямі, що лежать на одній площині, можуть перетинатися в одній точці, або не  перетинатися.

 

Прямі, які перетинаються - прямі, які мають спільну точку. Цю точку називають точкою перетину.

Якщо прямі лежать на одній площині й не перетинаються, то їх називають паралельними.

Назва походить від грецького слова «паралелос» (παράλληλος), що означає «йдуть поруч».

Позначення паралельних прямих: AB || CD

Цей запис читають так: «Пряма AB паралельна прямій CD».

 

Якщо AB || CD, то CD || AB.

Інший спосіб для запису паралельних прямих — a || b.

Вправа № 1522,1528

02.05.Перпендикулярні і паралельні прямі.

Дві прямі, що перетинаються під прямим кутом, називаються перпендикулярними.

  

Скорочено це записують так: a⊥b

Відрізки або промені називаються перпендикулярними, якщо вони лежать на перпендикулярних прямих.

Теорема (про дві прямі, перпендикулярні до третьої).

Дві прямі, перпендикулярні до третьої, паралельні.

Перпендикуляром до даної прямої, проведеним із точки A, називається відрізок прямої, перпендикулярної до даної, одним із кінців якого є точка А, а другим (основою перпендикуляра) — точка перетину цих прямих.

Відстанню від точки до прямої, яка не проходить через дану точку, називається довжина перпендикуляра, проведеного з даної точки до даної прямої.

Запам'чтай основні поняття. Виконай вправи №1513,1517

30.04. Контрольна робота

1. Спростіть  вираз:   2а∙2b    (1бал)

2. Розкрийте дужки:  3(2а-6)  (1бал)

3. Зведіть  подібні  доданки:  10-5b-12+5b    (1бал)

4. Винесіть  за  дужки спільний  множник:   1,3а+1,3n      (1бал)

5.Розв'яжіть  рівняння:          9х-14=4   (1бал)

6.Розкрийте  дужки  і  зведіть подібні  доданки:  12х-(3х+6)   (1бал)

7. Спростіть  вираз :    -3,5(4а-2b)+2,4(3а-5,2b)        (2 бали)

8. Розв'яжіть  рівняння :         0,5(3х-5)=8-0,4(6-2,5х)      (2 бали)

9. Розв'яжіть   задачу склавши  рівняння:

        Автобус і  легковий  автомобіль, швидкість якого на 19 км/год більша від швидкості автобуса, виїхали одночасно назустріч одне одному із двох міст, відстань між якими складає 477 км. Визначте  швидкості автобуса та  легкового  автомобіля  якщо відомо, що вони зустрілися через 3 год після виїзду.  (2 бали)

23.04.Застосування рівнянь до розв’язування задач на рівність двох величин

Д/з. Вивчати § 30 , виконати №1255,1463

18.04. Рівняння. Основні властивості рівнянь.

Переглянь відео:

Виконай: №1432

16.04.Вирази та їх спрощення.

Виконай № 1404, 1406

11.04.                                     Контрольна робота

Множення та ділення раціональних чисел

1. Обчисли:

а) – 16 · 0,5;             б) – 7,5 · ( - 1);         в)  · ( - 0,8 );

г) – 3,7 · 0,01;          д) – 4  · ( - 5  );      е) – 22,8 : ( - 0,38);

ж) -  : 0,6;              і) – 1 : 0,2;                 к) – 8  : ( - 1  ).

      2.   Розв’яжи рівняння:

           а) – 2,5 ( 5,7 – х ) = 0;        

           б) х :  = - 1 ;                       в) – х : ( - 2,4 ) = 3,05;

    3. Знайди значення виразів:

             б)  9  : 19 – 12,7 : ( - 10 ) + 11  : 14

09.04. Ділення раціональних чисел.

Пам'ятай головне!

Д/з №1343

2-4.04. Множення раціональних чисел

Запам'ятай правило!

 Щоб перемножити два числа з різними знаками, потрібно:

• перемножити модулі цих чисел;
  
  
• перед отриманим числом поставити знак «−».

Щоб перемножити два від'ємні числа, потрібно перемножити їхні модулі.

№1302,1304

19.03.Віднімання раціональних чисел.

Різницею раціональних чисел a і b називають таке число x, яке в сумі із числом b дає число a. Щоб від одного числа відняти друге, достатньо до зменшуваного додати число, протилежне від'ємнику: a − b = a + ( − b ) , або a − ( − b ) = a + b .

Виконуємо № 1203,1221

14.03. Додавання раціональних чисел.

Повторюємо правило додавання раціональних чисел. Виконуємо №1163, 1170

12.03.Додавання раціональних чисел.

Запам'ятай! Щоб знайти суму двох чисел з різними знаками, потрібно:знайти модулі доданків;із більшого модуля відняти менший модуль;перед отриманим числом поставити знак того з доданків, модуль якого більший. Сума протилежних раціональних чисел дорівнює нулю-5+5=07+(-7)=0

Виконай: № 1133, 1142

07.03.Раціональні числа.

 Запам'ятай!

Цілі числа (додатні і від'ємні), дробові числа (додатні і від'ємні) та число 0 називають раціональними числами.

Виконай: №1088,1097

15.02. Перетворення звичайного дробу в десятковий. Періодичні дроби.

№561,570

13.02 Перетворення звичайного дробу в десятковий.

№559

30.01. Ділення дробів.

Правило!

Щоб поділити один дріб на інший, треба ділене помножити на число, обернене дільнику.

 ab:cd=ab⋅dc=a⋅db⋅c

№ 498

25.01. Множення дробів.

Переглянь відео. 

Запам'ятай правило:

Щоб помножити дріб на дріб, треба:

• знайти добуток чисельників і добуток знаменників;
• перший добуток записати чисельником, а другий — знаменником.

ab⋅cd=a⋅cb⋅d

Приклад:

45⋅211=4⋅25⋅11=855

 

При потребі дріб скорочують.

Виконай № 435

23.01. Множення дробів.

Время: 23 янв. 2024 11:15 AM Europe/Kyiv

https://us04web.zoom.us/j/75513015551?pwd=PRRmMFJ82ReVCLbcmPw9QgmjxUbe5E.1

 755 1301 5551

Код доступа: 1CGag1

Д/з № 434,436

21.12.Додавання і віднімання мішаних чисел.

Онлайн урок  о 11.15

https://us04web.zoom.us/j/3236928986?pwd=uMmakuYMzOe3XhlHn4bJbLLPMbR24e.1

 323 692 8986

 0701

Виконуємо. № 389(1,4,7), 391(1,3,5), 395 

Д/з № 396

19.12.Додавання і віднімання дробів з різними знаменниками.

Онлайн урок  о 9.30

https://us04web.zoom.us/j/3236928986?pwd=uMmakuYMzOe3XhlHn4bJbLLPMbR24e.1

 323 692 8986

 0701

14.12.Додавання і віднімання дробів з різними знаменниками.

Онлайн урок  о 11.15. 

https://us04web.zoom.us/j/3236928986?pwd=uMmakuYMzOe3XhlHn4bJbLLPMbR24e.1

 323 692 8986

 0701

  Щоб звести дроби до найменшого спільного знаменника, треба:

1)    знайти найменший спільний знаменник даних дробів (найменше спільне кратне знаменників, НСК);

2)    знайти додаткові множники для кожного з дробів, поділивши спільний знаменник на знаменники даних дробів;

3)    помножити чисельник і знаменник кожного дробу на його додатковий множник.

№ 379,389,391

Д/з № 390

12.12.Додавання дробів з різними знаменниками.

Онлайн урок  о 9.40. 

https://us04web.zoom.us/j/3236928986?pwd=uMmakuYMzOe3XhlHn4bJbLLPMbR24e.1

 323 692 8986

 0701

Продовуємо розв'язувати вправи на додавання та віднімання дробів з різними знаменниками.

Виконуємо на уроці: № 373, 381.

Домашнє завдання: № 382

5-7.12. Додавання дробів з різними знаменниками.

 Щоб додати два дроби з однаковими знаменниками, треба додати їхні чисельники, а знаменник залишити той самий:

           

  Щоб відняти дроби з однаковими знаменниками, треба від чисельника зменшуваного відняти чисельник від'ємника, а знаменник залишити той самий:

             

  Щоб звести дроби до найменшого спільного знаменника, треба:

1)    знайти найменший спільний знаменник даних дробів (найменше спільне кратне знаменників, НСК);

2)    знайти додаткові множники для кожного з дробів, поділивши спільний знаменник на знаменники даних дробів;

3)    помножити чисельник і знаменник кожного дробу на його додатковий множник.

Онлайн урок о 11.15.

Ідентифікатор конференції: 719 3413 7573

Код доступу: 8jaJJK

Виконуємо разом № 371, 373,375

Д/З  №372

 21-23.11. Зведення дробів до спільного знаменника.

Число, яке одночасно ділиться на задані, це спільне кратне.

 

Щоб звести дроби до спільного знаменника потрібно обрати спільне кратне і помножити чисельник і знаменник дробу на число, щоб в знаменнику отримати число рівне обраному спільному знаменнику.

Приклад:

Найчастіше для роботи з дробовими числами вибирають найменший спільний знаменник.

Щоб отримати дроби зі спільними знаменниками потрібно їх помножити на певне число.

Щоб знайти додатковий множник потрібно найменший спільний знаменник поділити на знаменник дробу. 

Переглянь відео.

Спробуй виконати вправи  №332,333